MLLab[1]: Linear Regression

Basic Data Operate

1
2
3
4
5
6
7
8
%pip install seaborn
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt # matplotlib.pyplot是一些命令行风格函数的集合，使matplotlib以类似于MATLAB的方式工作。
import seaborn as sns
sns.set(context="notebook", style="whitegrid", palette="deep")
A=np.eye(5)    #单位对角矩阵
print(A)

Output：

1
2
3
4
5
6
7
df = pd.read_csv('ex1data1.txt',names=['人口','利润'])    # header = None表示没有表头
#需要注意的是，Jupyter notebook只能打开当前目录下的数据集，如csv，所以需要使用upload把数据集倒导入到当前目录下。           
#pd.read_csv的作用是将csv文件读入并转化为数据框形式，有非常多的参数，用到时可查阅文档。

df.head() #读前5行
#括号内可填写要读取的前n行，如果不填，默认为n=5
df.info() #查看索引、数据类型和内存信息

Output:)

Data Visualize

1
2
#fit_reg:拟合回归参数,如果fit_reg=True则散点图中则出现拟合直线
plt.show())

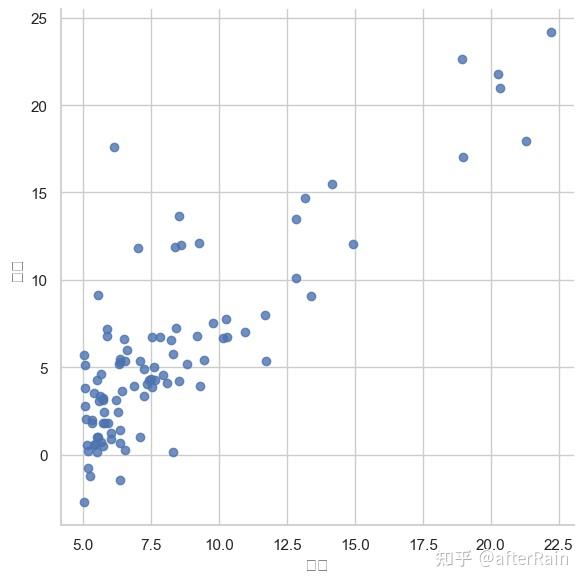
computeCost

1
2
3
4
5
6
7
8
9
10
11
def computeCost(X,y,theta):
    inner=np.power((X*theta-y),2)
    return np.sum(inner)/(2*len(X))
df.insert(0,'ONE',1)
cols = df.shape[1]
X = df.iloc[:,0:cols-1]
y = df.iloc[:,cols-1:cols]
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0]
computeCost (X,y,theta)))

Output：np.float64(32.072733877455676)

gradientDescent

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def gradientDescent(X,y,theta,alpha,iters):      #alpha是学习率,iters为迭代次数
    temp=np.matrix(np.zeros(theta.shape)) #np.zeros(theta.shape)=[0.,0.],然后将temp变为矩阵[0.,0.]
    parameters= int(theta.ravel().shape[1])  
    #theta.ravel()：将多维数组theta降为一维，.shape[1]是统计这个一维数组有多少个元
    #parameters表示参数
    cost=np.zeros(iters)     #初始化代价函数值为0数组，元素个数为迭代次数

    for i in range(iters):   #循环iters次
        error=(X*theta.T)-y


        for j in range(parameters):
            term = np.multiply(error, X[:,j])  #将误差与训练数据相乘，term为偏导数，参考笔记P27
            temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term)) #更新theta


        theta=temp
        cost[i] = computeCost(X,y,theta)  #计算每一次的代价函数

    return theta,cost

alpha=0.01
iters=1500
g, cost = gradientDescent(X, y, theta, alpha, iters) #令g和cost分别等于函数的两个返回值

Linear Regression Visualize

1
2
3
4
5
6
7
8
9
10
11
12
x = np.linspace(df.人口.min(),df.人口.max(),100)#以人口最小值为起点，最大值为终点，创建元素个数为100的等差数列
f = g[0,0] + (g[0,1] * x) #f是假设函数H

fig, ax = plt.subplots(figsize=(12,8))#以其他关键字参数**fig_kw来创建图
#figsize=(a,b):figsize 设置图形的大小,b为图形的宽,b为图形的高,单位为英寸
ax.plot(x, f, 'r', label='Prediction')   #设置点的横坐标，纵坐标，用红色线，并且设置Prediction为关键字参数
ax.scatter(df.人口, df.利润, label='Traning Data')  #以人口为横坐标，利润为纵坐标并且设置Traning Data为关键字参数
ax.legend(loc=2)  #legend为显示图例函数，loc为设置图例显示的位置，loc=2即在左上方
ax.set_xlabel('Population')  #设置x轴变量
ax.set_ylabel('Profit')  #设置x轴变量
ax.set_title('Predicted Profit vs. Population Size') #设置表头
plt.show()

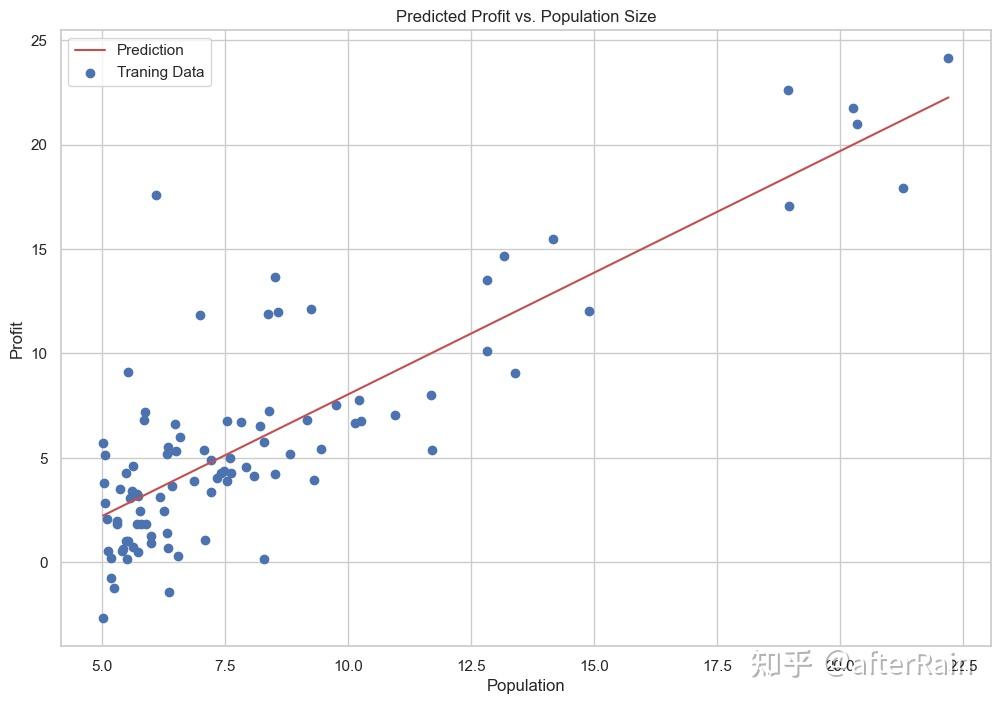
1
2
3
4
5
sns.lineplot(x=np.arange(iters), y=cost)
plt.xlabel("Iterations")
plt.ylabel("Cost")
plt.title("Cost vs. Iterations")
plt.show()

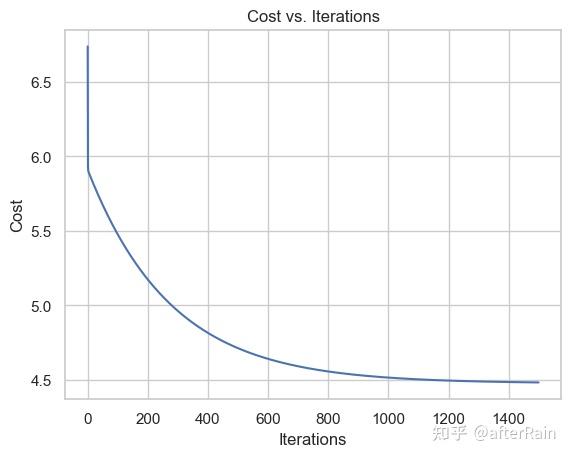
Other Situation

  • scikit-learn
1
2
3
from sklearn import linear_model  #从sklearn库中引入线性模块 
model = linear_model.LinearRegression()  #声明对象为线性回归模型
model.fit(np.asarray(X), np.asarray(y))  #拟合X,y，先转换为numpy数组
1
2
3
4
5
6
7
8
9
10
11
12
x = np.array(X[:, 1].A1)
f = model.predict(np.asarray(X)).flatten() #将model.predict(X)中的数据降为一维，并返回源数据的副本

fig, ax = plt.subplots(figsize=(12,8))#以其他关键字参数**fig_kw来创建图
#figsize=(a,b):figsize 设置图形的大小,b为图形的宽,b为图形的高,单位为英寸
ax.plot(x, f, 'r', label='Prediction')   #设置点的横坐标，纵坐标，用红色线，并且设置Prediction为关键字参数
ax.scatter(df.人口, df.利润, label='Traning Data')  #以人口为横坐标，利润为纵坐标并且设置Traning Data为关键字参数
ax.legend(loc=2)  #legend为显示图例函数，loc为设置图例显示的位置，loc=2即在左上方
ax.set_xlabel('Population')  #设置x轴变量
ax.set_ylabel('Profit')  #设置x轴变量
ax.set_title('Predicted Profit vs. Population Size') #设置表头
plt.show()
  • Normal Equation
1
2
3
4
5
6
# 正规方程
def normalEqn(X, y):
    theta = np.linalg.inv(X.T@X)@X.T@y#X.T@X等价于X.T.dot(X)  .dot()表示点积，也就是矩阵相乘的意思
    return theta
final_theta2=normalEqn(X, y)#感觉和批量梯度下降的theta的值有点差距
final_theta2

v2-ea41a180af38f5a2f510cfc4d9421b12_1440w

  • 梯度下降：需要选择学习率α，需要多次迭代，当特征数量n大时也能较好适用，适用于各种类型的模型
  • 正规方程：不需要选择学习率α，一次计算得出，需要计算，如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为O(n3)，通常来说当n小于10000 时还是可以接受的，只适用于线性模型，不适合逻辑回归模型等其他模型